DAG가 뭔가요? 🤔

Q. DAG가 뭔가요?

A : DAG는 다들 아시다시피 directed acyclic graph 입니다.

Q. 그래서 directed acyclic graph 가 뭔가요?

A : directed graph 가 directed cycles를 가지지 않았으면 DAG 입니다.

Q. 그러면 directed graph와 directed cycles가 뭔가요?

먼저 directed graph 의 정의부터 보면…

Def. In formal terms, a directed graph is an ordered pair G = (V, A) where

• V is a set whose elements are called vertices, nodes, or points;
• A is a set of ordered pairs of vertices, called arrows, directed edges (sometimes simply edges > with the corresponding set named E instead of A), directed arcs, or directed lines.

아, 영어라 머리가 아파요… 한글로 보시죠..

유향 그래프는 $\Gamma =(V,E)$는 집합 $V$와, $V$의 순서쌍들로 구성된 집합 $E\subset V\times V$의 순서쌍이다.

이 경우, $e=(u,v)$라면 $e$를 $u$에서 $v$로 가는 변이라고 하며, 꼭짓점 $v$는 변 $e$의 머리, 꼭짓점 $u$는 변 $e$의 꼬리라고 한다.

쉽게 얘기해서 방향이 있는 그래프네요.

그럼 directed cycles는 뭘까요?

A directed cycle graph is a directed version of a cycle graph, with all the edges being oriented in the same direction.

아, 방향이 있는 순환 그래프이네요! 모든 edge가 같은 방향을 가지고 있는거네요!

Def. A directed cycle in a directed graph $G$ is a path $v_1, v_2, …, v_k$ in $G$ in which $v_1 = v_k, k > 2$, and the first $k-1$ nodes are all distinct.

라고도 다른데서 정의하는 걸로 봐서는 같은 걸 의미하네요!

정리해봅시다.

DAG는 directed graph 가 directed cycles를 가지지 않은 것이며,

방향이 있는 그래프에서 방향이 있는 순환 그래프를 포함하지 않으면 되는 거네요!

Def. A DAG is a directed graph that contains no directed cycles

(Example of a directed acyclic graph, https://en.wikipedia.org/wiki/Directed_acyclic_graph)

어쩐지 이름부터가 Directed Acyclic Graph(유향 비순환 그래프) 였네요.

Q. 이거 어디서 본 것 같아요!

A. 아, 위상 정렬(Topological Sorting) 을 아시는군요!

네? 모르는데요…

모르시면, 정의부터 봐야겠네요 ㅎㅎ

그럼 위상 정렬(Topological Sorting) 의 정의는 뭘까요?

그래프 이론 책이 없어서 위키피디아를 또 찾아가보겠습니다.

In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.

Def. A topological ordering of a directed graph $G = (V, E)$ is an ordering of its nodes as $v_1, v_2, …, v_n$ so that for every edge $(v_i, v_j)$ we have $i < j$.

오 명확해졌습니다!

Directed graph의 topological ordering 이란,

모든 vertices의 선형 정렬인데, 모든 directed edge (u, v) 들에 대해서, u는 무조건 v 전에 선행한다는 거네요!

즉, 다시 말하면

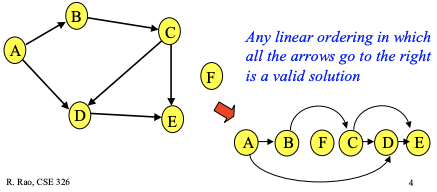
처럼 선형으로 표현가능하지만, 같은 그래프를

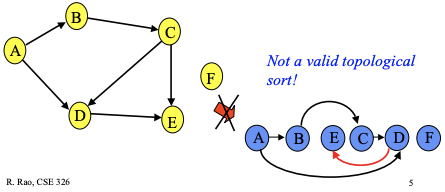
처럼 정렬하면 안된다는 겁니다.

왜냐하면, D → E edge가 있지만, E가 D보다 선행되었기 때문이죠.

그런데 앞에 소개한 둘이 사실 같은게 아닌가요?

네, 같아 “보입니다.”

그런데 진짜 같은 걸까요?

정확히 어떤게 같다고 표현해야할까요?

명제를 만들어봅시다.

우선 앞에서 정의한 두 친구를 데려와 봅시다.

DAG 란, directed graph 가 directed cycles를 가지지 않은 것입니다.

Topological Sorting이란, directed graph들의 vertexs를 edge의 방향에 거스르지 않고 나열한 것입니다.

두 친구 모두 directed graph 에 대해서 얘기를 하고 있네요.

그럼 증명할 명제를 만들어보면…

For a directed graph G, G is a DAG if and only if G has a topological order

가 됩니다!

그러면 이제 위의 명제를 증명하면 됩니다.

명제를 증명해봅시다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

Lemma. For a directed graph G, if G has a topological order, then G is a DAG.

Pf. (by contraction)
Suppose that G has a topological order.
Suppose that G has a directed cycle C.

Let vi be the lowest-indexed vertex in C
and let vj be the vertex just before vi in C.
thus, (vj, vi) is an edge.

WLOG, we have i < j.

On the other hand, Since (vj, vi) is an edge and v1,... ,vn is a topological order,
we must have j < i. (-><-)

So, G has a no directed cycle.
Therefore, G is a DAG.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

Lemma. For a directed graph G, if G is a DAG, then G has a topological order.

Pf. (by induction on i)
(i = 1) true, because topological ordering is G.
(i = n + 1)
Suppose that if G is a DAG of size <= n, G has a topological order.

Given DAG G with n+1 vertexs.
Let v be a vertex with no incoming edges.

G - {v} is a DAG, since deleting v cannot create cycles.
By hypothesis, G - {v} has a topological order.

Create topological ordering for G:
 - Place v first; then append topological ordering of G - {v}
 - This is valid since v has no incoming edges.

By induction, the lemma is proven.

많이 본 모양인데 말이죠… 어디서 봤을까요?

• Genealogy and version history
  • Git branch 의 구조가 DAG네요.

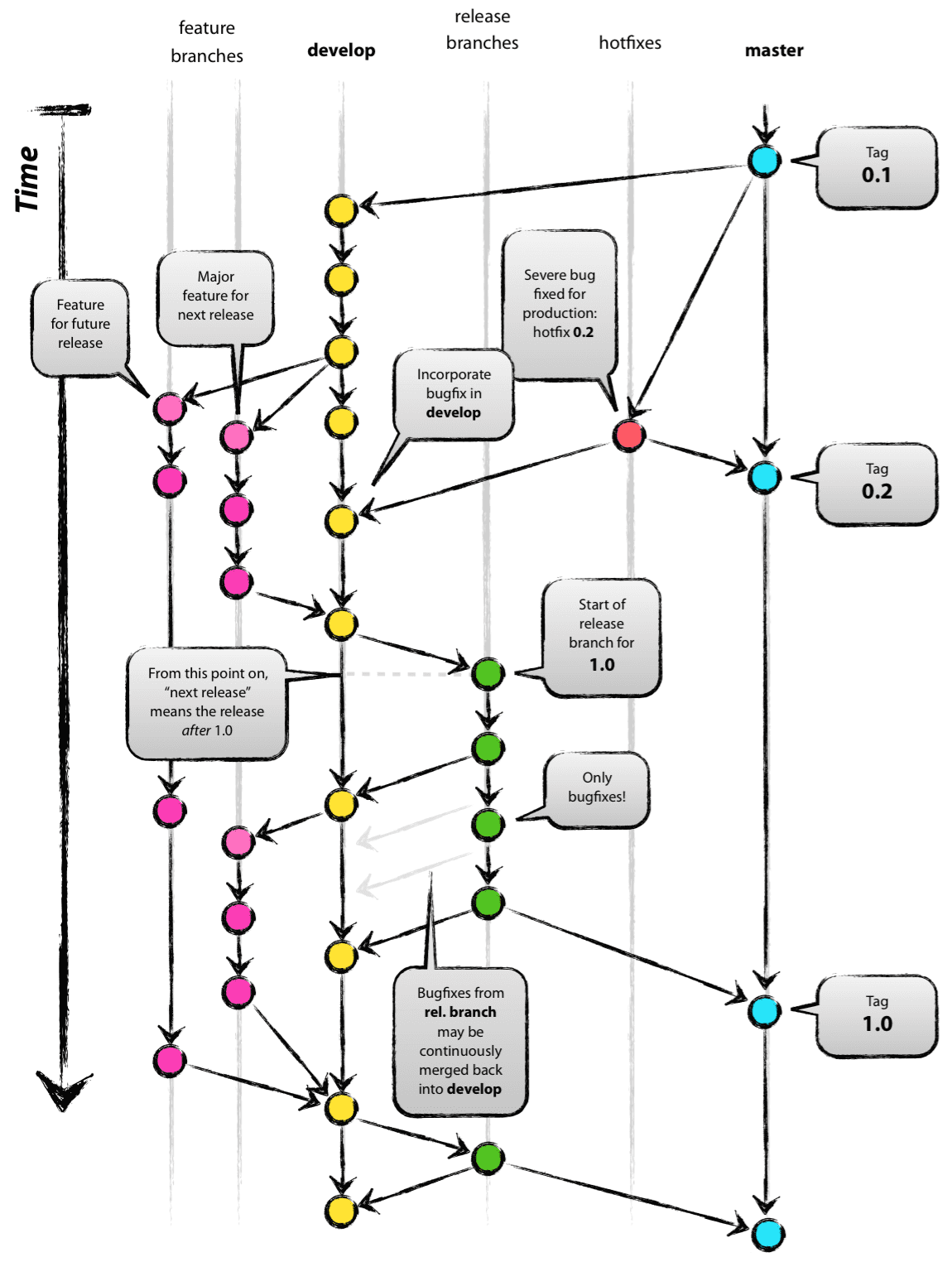
• Scheduling

• Data processing networks
• Data compression

그런데 왜 이걸 했을까요? 🤔

Git branch 의 그래프 구조가 어떤건지 궁금해서 찾아봤습니다 🙂

References

• https://en.wikipedia.org/wiki/Directed_acyclic_graph
• https://ko.wikipedia.org/wiki/순환_그래프
• https://en.wikipedia.org/wiki/Topological_sorting
• https://ko.wikipedia.org/wiki/위상정렬
• https://ocw.tudelft.nl/wp-content/uploads/Algoritmiek_DAGs_and_Topological_Ordering.pdf